Kruskal-Wallis Test Explained with Example and Use Cases

Introduction

• The Kruskal-Wallis test (H test) is a non-parametric statistical test used to compare three or  more independent groups and to determine if there are statistically significant differences between them. It is an extension of the Mann-Whitney U test, which is used for comparing two groups.
• This test is an alternative of Analysis of variance(ANOVA) when the data are not normally distributed.
• It gives significant result when at least one of the samples is different from other samples.

Objectives

1. To understand the Kruskal-Walli’s test and its significance.
2. To apply the test to a real-world dataset.
3. To interpret the results and conclude whether there are significant differences between groups.
4. How to perform the test using SPSS

Theoretical Background

When to Use the Kruskal-Wallis Test

• The data is not normally distributed.
• The dependent variable is ordinal or continuous.

M1,M2…. MK are the median value of 1^st and 2^nd…. Kth group of samples then,

Hypotheses

• Null Hypothesis (H₀): The medians of all groups are equal. Or    H₀= M1=M2=…. MK
• Alternative Hypothesis (H₁): At least one group has a different median.

Formula for Kruskal-Wallis Test Statistic (H)

The test statistic is calculated using:

H = (12 / (N(N + 1))) × Σ(Rᵢ² / nᵢ) - 3(N + 1)

where:

• N = total number of observations
• <span style="font-size: 1rem;">Ri = sum of ranks for ith group</span>
• ni = number of observations in group i

The H statistic is compared to a critical value from the chi-square distribution with k−1 degrees of freedom (where k is the number of groups). If Calculated value is greater than table value we reject the null hypothesis.

Example: Effect of Fertilizers on Plant Growth

Scenario

A researcher wants to determine if different fertilizers affect plant growth. Three fertilizers (A, B, and C) are used, and plant heights (in cm) are measured after four weeks

Data Collection

Fertilizer A	Fertilizer B	Fertilizer C
10	15	18
12	17	21
14	19	23
13	20	20

Step 1: Rank the Data

Value	Group	Rank
10	A	1
12	A	2
13	A	3
14	A	4
15	B	5
17	B	6
18	C	7
19	B	8
20	B	9.5
20	C	9.5
21	C	11
23	C	12

Step 2: Compute Rank Sums

RA=1+2+3+4=10
RB=5+6+8+9.5=28.5
RC=7+9.5+11+12=39

Step 3: Compute the H Statistic

Substituting values into the formula:

H = [12 / (12 × 13)] × [(10² / 4) + (28.5² / 4) + (39.5² / 4)] - 3 × 13

After calculation, <strong>H = 8.5</strong> .

Step 4: Compare with Critical Value

• Degrees of Freedom (df) = K-1 = 3-1 =2
  Chi-square critical value at α = 0.05 is 5.99.
  Since <strong>H = 8.5 > 5.99</strong>, we reject the null hypothesis.

Step 5: Interpretation

Since the Kruskal-Walli’s test result is significant, it means at least one fertilizer has a different effect on plant growth.

Conclusion

Significant Differences in Plant Growth Among Different Fertilizers.

References

1. Kruskal, W. H., & Wallis, W. A. (1952). “Use of Ranks in One-Criterion Variance Analysis.” Journal of the American Statistical Association.
2. Conover, W. J. (1999). “Practical Nonparametric Statistics.” Wiley.
3. McDonald, J. H. (2014). “Handbook of Biological Statistics.” Sparky House Publishing.

Kruskal-Wallis Test in SPSS

Step 1: Enter the Data

1. Open SPSS and go to Variable View.
2. Create two variables:
   • “Fertilizer” (Categorical: A, B, C) Measure Type: Nominal
     Explanation: Fertilizer is a categorical variable (A, B, or C), meaning it represents different groups without any inherent order.
   • “Plant Height” (Scale: Continuous height values) Measure Type: Scale (Continuous)
     Explanation: Plant height is a numeric variable with measurable values, making it a scale variable in SPSS.

Step 2: Run the Kruskal-Wallis Test

Click Analyse > Nonparametric Tests > Legacy Dialogs >Independent Samples. Fields>Move "Plant Height" to the Test Variable List>Move "Fertilizer" to the Grouping Variable>Settings>select Kruskal walli’s test>Ok

Step 3: Interpret the Output

Independent-Samples Kruskal-Wallis Test Summary
Total N	12
Test Statistic	8.578a
Degree Of Freedom	2
Asymptotic Sig.(2-sided test)	.014
a. The test statistic is adjusted for ties.

H = 8.5 (same as our manual calculation).

df = 2 (since we have 3 groups, df = k−1k – 1k−1).

p-value = 0.014 (which is less than 0.05, indicating statistical significance).

Box Plot (Graphical Representation)

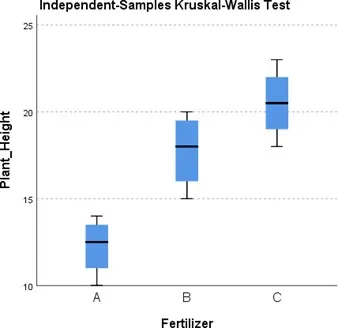
• The box plot visually represents the distribution of plant heights across the three fertilizer groups.
• It helps in understanding the median, spread, and potential outliers.

Final Interpretation

• p-value = 0.014 < 0.05, we reject the null hypothesis.
• This means that at least one fertilizer significantly affects plant growth.

Pairwise Comparisons of Fertilizer
Sample 1-Sample 2	Test Statistic	Std. Error	Std. Test Statistic	Sig.	Adj. Sig.a
A-B	-4.625	2.545	-1.817	.069	.208
A-C	-7.375	2.545	-2.898	.004	.011
B-C	-2.750	2.545	-1.081	.280	.840
Asymptotic significances (2-sided tests) are displayed. The significance level is .05.
a. Significance values have been adjusted by the Bonferroni correction for multiple tests.

Interpretation of Results

1. A vs. B
   • p= 0.069 (unadjusted) and 0.208 (Bonferroni-adjusted).
   • Since p > 0.05, there is no significant difference between Fertilizer A and B.
2. A vs. C
   • p = 0.004 (unadjusted) and 0.011 (Bonferroni-adjusted).
   • Since p < 0.05, there is a significant difference between Fertilizer A and C.
   • This suggests that Fertilizer C has a significantly different effect on plant height compared to A.
3. B vs. C
   • p = 0.280 (unadjusted) and 0.840 (Bonferroni-adjusted).
   • Since p > 0.05, there is no significant difference between Fertilizer B and C.

Final Conclusion

• Fertilizer A and C show a statistically significant difference, indicating that one is more effective than the other in promoting plant growth.
• No significant differences are observed between A and B or between B and C.